Introduction to Pumas

This is an introduction to Pumas, a software system for pharmaceutical modeling and simulation. Pumas supports NLME (non-linear mixed effects models) estimation and simulation, NCA (non-compartmental analysis), Bioequivalence analysis, optimal design, and more.

In this tutorial we focus on NLME. The basic workflow of NLME with Pumas is:

1. Build a model.
2. Define subjects or populations to simulate or estimate.
3. Analyze the results with post-processing and plots.

We will show how to build a multiple-response PK/PD model via the @model macro, define a subject with single doses, and analyze the results of the simulation. Fitting of data using any of the methods available in Pumas is showcased in the tutorials. This tutorial is designed as a broad overview of the workflow and a more in-depth treatment of each section can be found in the tutorials.

Working Example

Let us start by showing complete simulation code, and then break down how it works.

using Pumas
using PumasUtilities
using CairoMakie

######### Turnover model

inf_2cmt_lin_turnover = @model begin
    @param begin
        tvcl ∈ RealDomain(; lower = 0)
        tvvc ∈ RealDomain(; lower = 0)
        tvq ∈ RealDomain(; lower = 0)
        tvvp ∈ RealDomain(; lower = 0)
        Ω_pk ∈ PDiagDomain(4)
        σ_prop_pk ∈ RealDomain(; lower = 0)
        σ_add_pk ∈ RealDomain(; lower = 0)
        # PD parameters
        tvturn ∈ RealDomain(; lower = 0)
        tvebase ∈ RealDomain(; lower = 0)
        tvec50 ∈ RealDomain(; lower = 0)
        Ω_pd ∈ PDiagDomain(1)
        σ_add_pd ∈ RealDomain(; lower = 0)
    end

    @random begin
        ηpk ~ MvNormal(Ω_pk)
        ηpd ~ MvNormal(Ω_pd)
    end

    @pre begin
        CL = tvcl * exp(ηpk[1])
        Vc = tvvc * exp(ηpk[2])
        Q = tvq * exp(ηpk[3])
        Vp = tvvp * exp(ηpk[4])

        ebase = tvebase * exp(ηpd[1])
        ec50 = tvec50
        emax = 1
        turn = tvturn
        kout = 1 / turn
        kin0 = ebase * kout
    end

    @init begin
        Resp = ebase
    end

    @vars begin
        conc := Central / Vc
        edrug := emax * conc / (ec50 + conc)
        kin := kin0 * (1 - edrug)
    end

    @dynamics begin
        Central' = -(CL / Vc) * Central + (Q / Vp) * Peripheral - (Q / Vc) * Central
        Peripheral' = (Q / Vc) * Central - (Q / Vp) * Peripheral
        Resp' = kin - kout * Resp
    end

    @derived begin
        dv ~ @. Normal(conc, sqrt((conc * σ_prop_pk)^2 + σ_add_pk^2))
        resp ~ @. Normal(Resp, σ_add_pd)
    end
end

turnover_params = (;
    tvcl = 1.5,
    tvvc = 25.0,
    tvq = 5.0,
    tvvp = 150.0,
    tvturn = 10,
    tvebase = 10,
    tvec50 = 0.3,
    Ω_pk = Diagonal([0.05, 0.05, 0.05, 0.05]),
    Ω_pd = Diagonal([0.05]),
    σ_prop_pk = 0.15,
    σ_add_pk = 0.5,
    σ_add_pd = 0.2,
);

regimen = DosageRegimen(150; rate = 10, cmt = :Central)
pop = map(i -> Subject(; id = i, events = regimen), 1:10)

Population
  Subjects: 10
  Observations: 

sd_obstimes = [
    # single dose observation times
    0.25,
    0.5,
    0.75,
    1,
    2,
    4,
    8,
    12,
    16,
    20,
    24,
    36,
    48,
    60,
    71.9,
];

sims = simobs(inf_2cmt_lin_turnover, pop, turnover_params; obstimes = sd_obstimes)

Simulated population (Vector{<:Subject})
  Simulated subjects: 10
  Simulated variables: dv, resp

sim_plot(
    inf_2cmt_lin_turnover,
    sims;
    observations = [:dv],
    figure = (; fontsize = 18),
    axis = (; xlabel = "Time (hr)", ylabel = "Concentration (ng/mL)"),
)

sim_plot(
    inf_2cmt_lin_turnover,
    sims;
    observations = [:resp],
    figure = (; fontsize = 18),
    axis = (; xlabel = "Time (hr)", ylabel = "Response"),
)

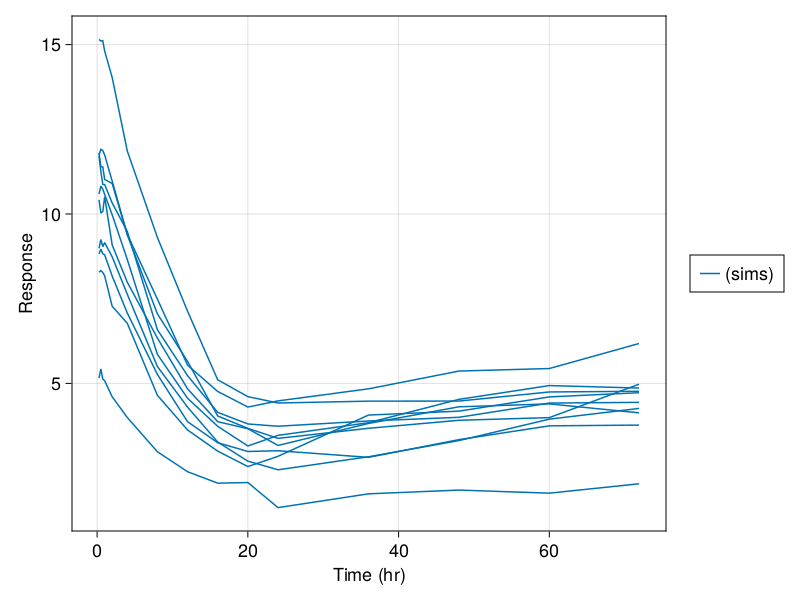
In this code, we defined a nonlinear mixed effects model by describing the parameters, the random effects, the dynamical model, and the derived (result) values. Then we generated a population of 10 subjects who received a single dose of 150 mg, specified parameter values, simulated the model, and generated a plot of the results. Now let's walk through this process!

Using the Model Macro

First we define the model. The simplest way to do this is via @model. Inside the @model block we have a few subsections. The first of these is a @param block.

@param

@model begin
  @param begin
    tvcl ∈ RealDomain(lower = 0)
    tvv ∈ RealDomain(lower = 0)
    Ω ∈ PDiagDomain(2)
    σ_prop ∈ RealDomain(lower = 0, init = 0.04)
  end
end

@emmodel begin
  @param begin
    CL ~ 1 + wt | LogNormal
    Vc ~ 1 | Normal
  end
end

For this model we define structural model parameters of PK and PD and their corresponding variances where applicable:

@param begin
    tvcl ∈ RealDomain(; lower = 0)
    tvvc ∈ RealDomain(; lower = 0)
    tvq ∈ RealDomain(; lower = 0)
    tvvp ∈ RealDomain(; lower = 0)
    Ω_pk ∈ PDiagDomain(4)
    σ_prop_pk ∈ RealDomain(; lower = 0)
    σ_add_pk ∈ RealDomain(; lower = 0)
    # PD parameters
    tvturn ∈ RealDomain(; lower = 0)
    tvebase ∈ RealDomain(; lower = 0)
    tvec50 ∈ RealDomain(; lower = 0)
    Ω_pd ∈ PDiagDomain(1)
    σ_add_pd ∈ RealDomain(; lower = 0)
end

Note the mathematical elegence of the expression of parameters, relationships, and distributions.

Next we define our random effects using the @random block.

@random

@model begin
  @random begin
    η ~ MvNormal(Ω)
  end
end

@emmodel begin
  @random begin
    CL ~ 1 + wt | LogNormal
    Vc ~ 1 | Normal
  end
end

The random effects are defined by a distribution from the Distributions package. For more information on defining distributions, please see the Distributions documentation. For this tutorial, we wish to have a multivariate normal of uncorrelated random effects, one for PK and another for PD, so we utilize the syntax:

@random begin
    ηpk ~ MvNormal(Ω_pk)
    ηpd ~ MvNormal(Ω_pd)
end

Now we define our pre-processing step in @pre.

@pre

@model begin
  @params begin
    tvcl ∈ RealDomain(lower = 0)
    tvv ∈ RealDomain(lower = 0)
    ωCL ∈ RealDomain(lower = 0)
    ωV ∈ RealDomain(lower = 0)
    σ_prop ∈ RealDomain(lower = 0, init = 0.04)
  end
  @random begin
    ηCL ~ Normal(ωCL)
    ηV ~ Normal(ωV)
  end
  @covariates wt
  @pre begin
    CL = tvcl * (wt / 70)^0.75 * exp(ηCL)
    Vc = tvv * (wt / 70) * exp(ηV)
    ka = CL / Vc
    Q = Vc
  end
end

For our PK/PD model, we define the individual parameters and their distributions, and we give them names as follows:

@pre begin
    CL = tvcl * exp(ηpk[1])
    Vc = tvvc * exp(ηpk[2])
    Q = tvq * exp(ηpk[3])
    Vp = tvvp * exp(ηpk[4])

    ebase = tvebase * exp(ηpd[1])
    ec50 = tvec50
    emax = 1
    turn = tvturn
    kout = 1 / turn
    kin0 = ebase * kout
end

Next we define the @init block which specifies the initial conditions of the dynamic system (i.e., initial compartment amounts).

@init

@model begin
  @init begin
    Depot1 = 0.0
    Depot2 = 0.0
    Central = 0.0
  end
end

Any variable not mentioned in this block is assumed to have a zero for its starting value. We wish to only set the starting value for Resp, and thus we use:

@init begin
    Resp = ebase
end

Now we define our dynamics. We do this via the @dynamics block.

@dynamics

@model begin
  @dynamics begin
    Depot1' = -ka * Depot1
    Depot2' = ka * Depot1 - ka * Depot2
    Central' = ka * Depot2 - CL / Vc * Central
  end
end

@model begin
  @dynamics Depots1Central1
end

For our PK/PD model, we specify the three differential equations that describe the PK and PD components of the system:

@dynamics begin
    Central' = -(CL / Vc) * Central + (Q / Vp) * Peripheral - (Q / Vc) * Central
    Peripheral' = (Q / Vc) * Central - (Q / Vp) * Peripheral
    Resp' = kin - kout * Resp
end

Note the convenience of expressing the compartment amounts by name and the value of the derivative equations using the single quote character.

Next we set up alias variables that can be used later in the code. Such alias code can be setup in the @vars block.

@vars

@model begin
  @vars begin
    conc = Central / Vc
  end
end

We create aliases for the concentration and response as follows:

@vars begin
    conc := Central / Vc
    edrug := emax * conc / (ec50 + conc)
    kin := kin0 * (1 - edrug)
end

Note that the local assignment := can be used to define intermediate statements that will not be carried outside the block. This means that all the resulting data workflows from this model will not contain the intermediate variables defined with :=. This optional use of local assignment improves computational efficiency.

Note that without adjustment the units of conc are the units of the dose divided by the units of the volume parameter. The balancing of conc units with those reported from the assay could occur here, but in this example we make this adjustment below in the @derived block.

Lastly we utilize the @derived block.

@derived

@model begin
  @derived begin
    dv ~ @. Normal(1000 * Central / Vc, 1000 * Central / Vc * σ)
  end
end

Our error model includes a component for each type of observation (i.e., conc and Resp):

@derived begin
    dv ~ @. Normal(conc, sqrt((conc * σ_prop_pk)^2 + σ_add_pk^2))
    resp ~ @. Normal(Resp, σ_add_pd)
end

Here dv (i.e., dependent variable) is the drug concentration and resp is the response. At any time that these outputs are sampled dv is normally distributed with mean conc and variance (conc * σ_prop_pk)^2 + σ_add_pk^2, and resp has mean Resp and a constant standard deviation σ_add_pd.

Building a Subject

Now let's build a subject to simulate the model with.

Subject

Subject(;id = "1",
         observations = NamedTuple(),
         events = nothing,
         time = observations isa AbstractDataFrame ? observations.time : nothing,
         covariates::Union{Nothing, NamedTuple} = nothing,
         covariates_time = observations isa AbstractDataFrame ? observations.time : nothing,
         covariates_direction = :left)

julia> Subject()
Subject
  ID: 1

julia> Subject(
         id = 20,
         events = DosageRegimen(200, ii = 24, addl = 2),
         covariates = (WT = 14.2, HT = 5.2),
       )
Subject
  ID: 20
  Events: 3
  Covariates: WT, HT

julia> Subject(covariates = (WT = [14.2, 14.7], HT = fill(5.2, 2)), covariates_time = [0, 3])
Subject
  ID: 1
  Covariates: WT, HT

Our model did not make use of covariates, so we will ignore covariate components covariates, covariate_time and covariate_direction for now, and observations are only necessary for fitting parameters to data which will not be covered in this tutorial. Thus, our subject will be defined simply by its dosage regimen.

To do this, we use the DosageRegimen constructor.

DosageRegimen(
  amt::Numeric;
  time::Numeric = 0,
  cmt::Union{Numeric,Symbol} = 1,
  evid::Numeric = 1,
  ii::Numeric = zero.(time),
  addl::Numeric = 0,
  rate::Numeric = zero.(amt)./oneunit.(time),
  duration::Numeric = zero(amt)./oneunit.(time),
  ss::Numeric = 0,
  route::NCA.Route = NCA.NullRoute,
)

julia> DosageRegimen(100; ii = 24, addl = 6)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1    100.0     1     24.0      6      0.0       0.0     0  NullRoute

julia> DosageRegimen(50; ii = 12, addl = 13)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1     50.0     1     12.0     13      0.0       0.0     0  NullRoute

julia> DosageRegimen(200; ii = 24, addl = 2)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1    200.0     1     24.0      2      0.0       0.0     0  NullRoute

julia> DosageRegimen(200; ii = 24, addl = 2, route = NCA.IVBolus)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1    200.0     1     24.0      2      0.0       0.0     0  IVBolus

evs = DosageRegimen(
  regimen1::DosageRegimen,
  regimen2::DosageRegimen;
  offset = nothing
)

julia> e1 = DosageRegimen(100; ii = 24, addl = 6)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1    100.0     1     24.0      6      0.0       0.0     0  NullRoute

julia> e2 = DosageRegimen(50; ii = 12, addl = 13)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1     50.0     1     12.0     13      0.0       0.0     0  NullRoute

julia> evs = DosageRegimen(e1, e2)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1    100.0     1     24.0      6      0.0       0.0     0  NullRoute
   2 │     0.0      1     50.0     1     12.0     13      0.0       0.0     0  NullRoute

julia> DosageRegimen(e1, e2; offset = 10)
DosageRegimen
 Row │ time     cmt    amt      evid  ii       addl   rate     duration  ss    route
     │ Float64  Int64  Float64  Int8  Float64  Int64  Float64  Float64   Int8  NCA.Route
─────┼───────────────────────────────────────────────────────────────────────────────────
   1 │     0.0      1    100.0     1     24.0      6      0.0       0.0     0  NullRoute
   2 │   178.0      1     50.0     1     12.0     13      0.0       0.0     0  NullRoute

For our example, let's assume the dose is a 150 mg infusion administered at the rate of 10 mg/hour into the Central compartment:

regimen = DosageRegimen(150; time = 0, rate = 10, cmt = :Central)

Let's define our subject to have id=1 with this single-dose regimen:

subject = Subject(; id = 1, events = regimen)

Subject
  ID: 1
  Events: 1

We can also create a collection of subjects which forms a population.

pop = map(i -> Subject(; id = i, events = regimen), 1:10)

Population
  Subjects: 10
  Observations: 

Running a Simulation

The main function for running a simulation is simobs.

simobs(
  model::AbstractPumasModel,
  population::Union{Subject, Population},
  param,
  randeffs=sample_randeffs(model, param, population);
  obstimes=nothing,
  ensemblealg=EnsembleSerial(),
  diffeq_options=NamedTuple(),
  rng=Random.default_rng(),
  simulate_error=Val(true),
)

randeffs = zero_randeffs(model, param, population)
solve(model, population, param, randeffs)

simobs(model::PumasModel, population::Population; samples::Int = 10, simulate_error = true, rng::AbstractRNG = default_rng())

simobs(model::PumasModel, subject::Subject; samples::Int = 10, simulate_error = true, rng::AbstractRNG = default_rng())

simobs(b::BayesMCMCResults; subject = nothing, samples::Int = 10, simulate_error = false, rng::AbstractRNG = default_rng())

simobs(pmi::FittedPumasModelInference, population::Population = pmi.fpm.data, randeffs::Union{Nothing, AbstractVector{<:NamedTuple}} = nothing; samples::Int, rng = default_rng(), kwargs...,)

simobs(fpm::FittedPumasModel, [population::Population,] vcov::AbstractMatrix, randeffs::Union{Nothing, AbstractVector{<:NamedTuple}} = nothing; samples::Int, rng = default_rng(), kwargs...)

Let's simulate subject 1 with a set of chosen parameters:

turnover_params = (;
    tvcl = 1.5,
    tvvc = 25.0,
    tvq = 5.0,
    tvvp = 150.0,
    tvturn = 10,
    tvebase = 10,
    tvec50 = 0.3,
    Ω_pk = Diagonal([0.05, 0.05, 0.05, 0.05]),
    Ω_pd = Diagonal([0.05]),
    σ_prop_pk = 0.15,
    σ_add_pk = 0.5,
    σ_add_pd = 0.2,
)

sims = simobs(inf_2cmt_lin_turnover, subject, turnover_params; obstimes = sd_obstimes)

SimulatedObservations
  Simulated variables: dv, resp
  Time: [0.25, 0.5, 0.75, 1.0, 2.0, 4.0, 8.0, 12.0, 16.0, 20.0, 24.0, 36.0, 48.0, 60.0, 71.9]

We can then plot the simulated observations by using the sim_plot function:

sim_plot(inf_2cmt_lin_turnover, sims; observations = :dv)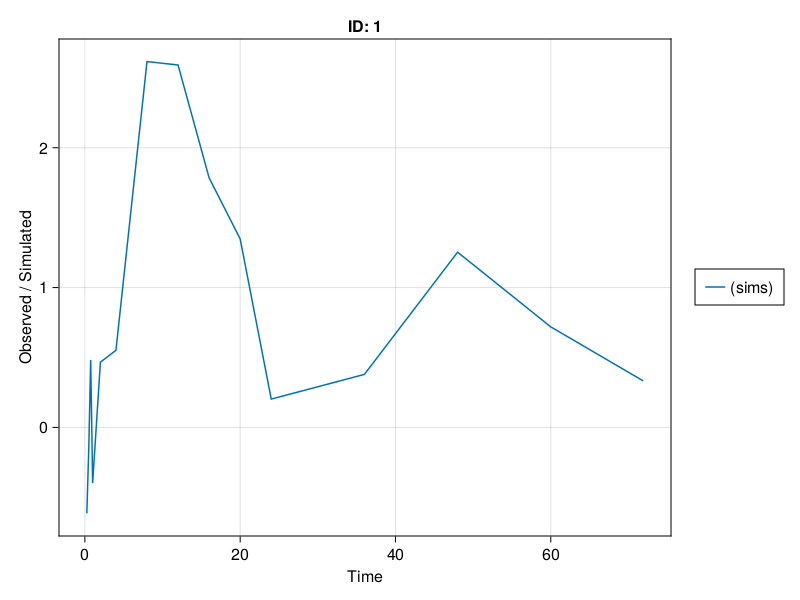

Note that we can further modify the plot, see Customizing Plots. For example,

sim_plot(
    inf_2cmt_lin_turnover,
    sims,
    observations = :dv,
    figure = (; fontsize = 18),
    axis = (; xlabel = "Time (hr)", ylabel = "Concentration (ng/mL)"),
)

When we only give the structural model parameters, the random effects are automatically sampled from their distributions. If we wish to prescribe a value for the random effects, we pass initial values similarly:

vrandeffs = [(; ηpk = rand(4), ηpd = rand()) for _ in pop]
sims =
    simobs(inf_2cmt_lin_turnover, pop, turnover_params, vrandeffs; obstimes = sd_obstimes)

Simulated population (Vector{<:Subject})
  Simulated subjects: 10
  Simulated variables: dv, resp

If a population simulation is required with the inter-subject random effects set to zero, then it is possible to use the zero_randeffs function:

etas = zero_randeffs(inf_2cmt_lin_turnover, turnover_params, pop)

sims = simobs(inf_2cmt_lin_turnover, pop, turnover_params, etas; obstimes = sd_obstimes)

fig = Figure(; resolution = (1000, 600), fontsize = 18)
ax1 = Axis(fig[1, 1]; xlabel = "Time (hr)", ylabel = "Concentration (ng/mL)")
ax2 = Axis(fig[1, 2]; xlabel = "Time (hr)", ylabel = "Response")
sim_plot!(ax1, inf_2cmt_lin_turnover, sims; observations = [:dv])

sim_plot!(ax2, inf_2cmt_lin_turnover, sims; observations = [:resp])

fig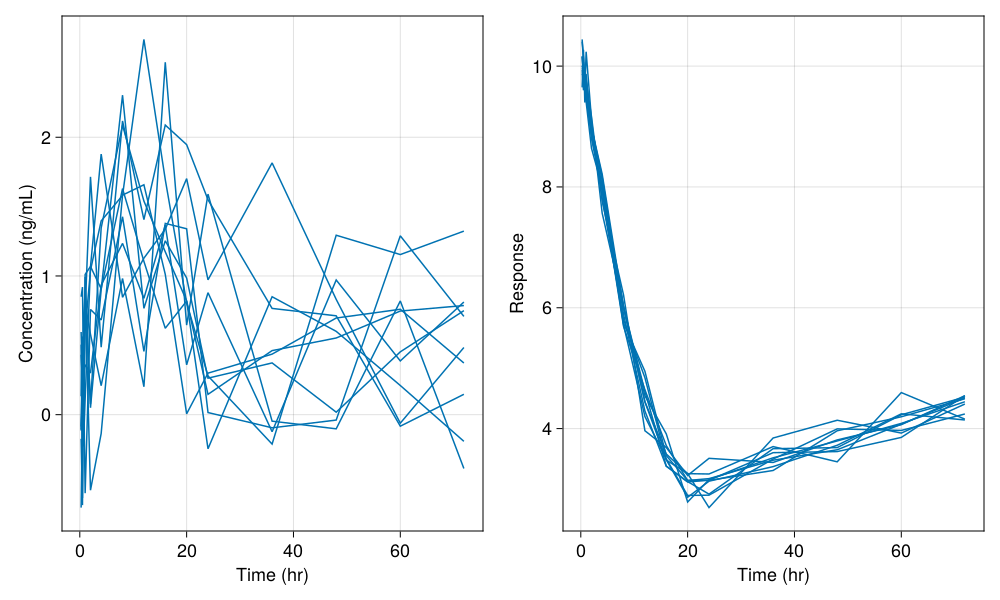

We still see variability in the plot above due to the residual variability components in the model. If we set the residual error variance parameters to tiny values as below

turnover_params_wo_sigma =
    (turnover_params..., σ_prop_pk = 1e-20, σ_add_pk = 1e-20, σ_add_pd = 1e-20)

(tvcl = 1.5,
 tvvc = 25.0,
 tvq = 5.0,
 tvvp = 150.0,
 tvturn = 10,
 tvebase = 10,
 tvec50 = 0.3,
 Ω_pk = [0.05 0.0 0.0 0.0; 0.0 0.05 0.0 0.0; 0.0 0.0 0.05 0.0; 0.0 0.0 0.0 0.05],
 Ω_pd = [0.05;;],
 σ_prop_pk = 1.0e-20,
 σ_add_pk = 1.0e-20,
 σ_add_pd = 1.0e-20,)

and perform the simulation without residual random effects we get only the population mean:

etas = zero_randeffs(inf_2cmt_lin_turnover, turnover_params, pop)

sims = simobs(
    inf_2cmt_lin_turnover,
    pop,
    turnover_params_wo_sigma,
    etas;
    obstimes = sd_obstimes,
)

fig = Figure(; resolution = (1000, 600), fontsize = 18)
ax1 = Axis(fig[1, 1]; xlabel = "Time (hr)", ylabel = "Concentration (ng/mL)")
ax2 = Axis(fig[1, 2]; xlabel = "Time (hr)", ylabel = "Response")

sim_plot!(ax1, inf_2cmt_lin_turnover, sims; observations = [:dv])

sim_plot!(ax2, inf_2cmt_lin_turnover, sims; observations = [:resp])

fig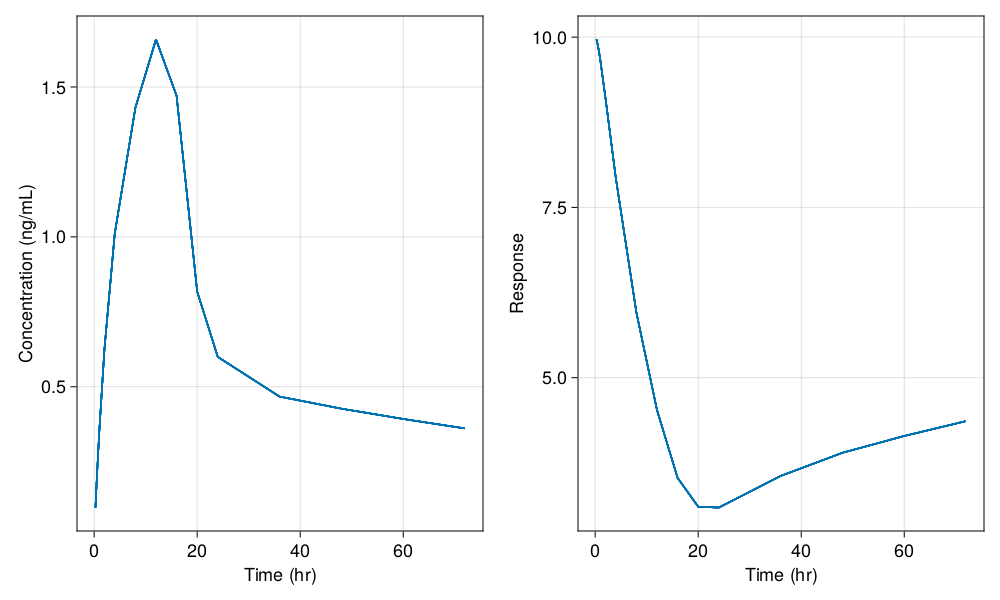

Handling the resulting simulation data

The resulting sims object contains the results of the simulation for each subject. The results for the ith subject can be retrieved by sims[i].

We can convert the simulation results to Pumas Subjects using the constructor broadcasted over all elements of sims:

sims_subjects = Subject.(sims)

Population
  Subjects: 10
  Observations: dv, resp

The newly created Subjects will contain the variables defined in the @derived-block as their observations. Then sims_subjects can be used to fit the model parameters based on the simulated dataset. We can also turn the simulated population into a DataFrame with the DataFrame constructor:

DataFrame(sims[1])

From there, any Julia tools can be used to analyze these arrays and DataFrames. Or you can conveniently export this to a CSV, Excel, or SAS data file.

Conducting an Estimation

With a model and population you can fit your model to your data. Model fitting in Pumas has the purpose of estimating parameters of a model, given a dataset, and is performed by calling the fit function with the following positional arguments:

1. a PumasModel constructed via @model, or a PumasEMModel constructed via @emmodel.
2. a Population or a Subject.
3. a named tuple of the initial parameter values.
4. an inference algorithm.

If you want to use the model's initial parameter values declared inside the @param block, you can do so with init_params(model). Note that this will fall back to the parameters' default values if you do not specify an initial value inside the @param block.

Pumas supports the following inference algorithms:

• Maximum Likelihood Estimation:

  • NaivePooled: first order approximation without inter-subject random-effects.
  • FO: first-order approximation.
  • FOCE: first-order conditional estimation.
  • LaplaceI: second-order Laplace approximation.
  • SAEM: Stochastic Approximation using the Expectation-Maximization algorithm. Note that for this you use @emmodel instead of @model.

• Bayesian inference:

  • BayesMCMC: MCMC using No-U-Turn Sampler (NUTS).
  • MarginalMCMC: MCMC using No-U-Turn Sampler (NUTS), but marginalizing out the subject-specific parameters.
  • MAP: Maximum A Posteriori estimation.

Now we can simultaneously fit our PK & PD models using one of the simulated populations from the previous section:

turnover_params = (;
    tvcl = 1.5,
    tvvc = 25.0,
    tvq = 5.0,
    tvvp = 150.0,
    tvturn = 10,
    tvebase = 10,
    tvec50 = 0.3,
    Ω_pk = Diagonal([0.05, 0.05, 0.05, 0.05]),
    Ω_pd = Diagonal([0.05]),
    σ_prop_pk = 0.15,
    σ_add_pk = 0.5,
    σ_add_pd = 0.2,
)

sims = simobs(inf_2cmt_lin_turnover, pop, turnover_params; obstimes = sd_obstimes)

Simulated population (Vector{<:Subject})
  Simulated subjects: 10
  Simulated variables: dv, resp

fit_2cmt_lin_turnover =
    fit(inf_2cmt_lin_turnover, Subject.(sims), init_params(inf_2cmt_lin_turnover), FOCE())

FittedPumasModel

Successful minimization:                      true

Likelihood approximation:                     FOCE
Likelihood Optimizer:                         BFGS
Dynamical system type:               Nonlinear ODE
Solver(s):                         (Vern7,Rodas5P)

Log-likelihood value:                   -156.74137
Number of subjects:                             10
Number of parameters:         Fixed      Optimized
                                  0             15
Observation records:         Active        Missing
    dv:                         150              0
    resp:                       150              0
    Total:                      300              0

--------------------------
              Estimate
--------------------------
tvcl           1.1682
tvvc          26.801
tvq            6.3267
tvvp         165.69
Ω_pk₁,₁        0.17137
Ω_pk₂,₂        0.091537
Ω_pk₃,₃        0.055024
Ω_pk₄,₄        2.9089e-74
σ_prop_pk      0.00084244
σ_add_pk       0.53685
tvturn         9.8483
tvebase       11.016
tvec50         0.28956
Ω_pd₁,₁        0.025593
σ_add_pd       0.21128
--------------------------

Calculating confidence intervals and Bootstrap

You can calculate confidence intervals using the infer function (by default 95% CIs):

infer_2cmt_lin_turnover = infer(fit_2cmt_lin_turnover)

Asymptotic inference results

Successful minimization:                      true

Likelihood approximation:                     FOCE
Likelihood Optimizer:                         BFGS
Dynamical system type:               Nonlinear ODE
Solver(s):                         (Vern7,Rodas5P)

Log-likelihood value:                   -156.74137
Number of subjects:                             10
Number of parameters:         Fixed      Optimized
                                  0             15
Observation records:         Active        Missing
    dv:                         150              0
    resp:                       150              0
    Total:                      300              0

------------------------------------------------
              Estimate       SE      95.0% C.I.
------------------------------------------------
tvcl           1.1682      NaN     [NaN; NaN]
tvvc          26.801       NaN     [NaN; NaN]
tvq            6.3267      NaN     [NaN; NaN]
tvvp         165.69        NaN     [NaN; NaN]
Ω_pk₁,₁        0.17137     NaN     [NaN; NaN]
Ω_pk₂,₂        0.091537    NaN     [NaN; NaN]
Ω_pk₃,₃        0.055024    NaN     [NaN; NaN]
Ω_pk₄,₄        2.9089e-74  NaN     [NaN; NaN]
σ_prop_pk      0.00084244  NaN     [NaN; NaN]
σ_add_pk       0.53685     NaN     [NaN; NaN]
tvturn         9.8483      NaN     [NaN; NaN]
tvebase       11.016       NaN     [NaN; NaN]
tvec50         0.28956     NaN     [NaN; NaN]
Ω_pd₁,₁        0.025593    NaN     [NaN; NaN]
σ_add_pd       0.21128     NaN     [NaN; NaN]
------------------------------------------------


Variance-covariance matrix could not be
evaluated. The random effects may be over-
parameterized. Check the coefficients for
variance estimates near zero.

You can also convert the output to a DataFrame with the coeftable function:

coeftable(infer_2cmt_lin_turnover)

The returned table also includes relative standard errors (RSEs). For inference with bootstrap-based confidence intervals you can use Bootstrap as an optional second positional argument in infer:

Bootstrap(; rng=Random.default_rng, samples=200, stratify_by=nothing, ensemblealg=EnsembleThreads())

Performing the bootstrap for our model can be performed as:

infer_boot_2cmt_lin_turnover =
    infer(fit_2cmt_lin_turnover, Bootstrap(; ensemblealg = EnsembleThreads()))

Bootstrap inference results

Successful minimization:                      true

Likelihood approximation:                     FOCE
Likelihood Optimizer:                         BFGS
Dynamical system type:               Nonlinear ODE
Solver(s):                         (Vern7,Rodas5P)

Log-likelihood value:                   -156.74137
Number of subjects:                             10
Number of parameters:         Fixed      Optimized
                                  0             15
Observation records:         Active        Missing
    dv:                         150              0
    resp:                       150              0
    Total:                      300              0

--------------------------------------------------------------------------------
              Estimate             SE                         95.0% C.I.
--------------------------------------------------------------------------------
tvcl           1.1682            0.26444           [  0.53796   ;   1.6056    ]
tvvc          26.801             6.5498            [ 19.663     ;  44.861     ]
tvq            6.3267            0.63479           [  5.5201    ;   7.9791    ]
tvvp         165.69             27.436             [119.75      ; 226.47      ]
Ω_pk₁,₁        0.17137           0.19149           [  0.051904  ;   0.64125   ]
Ω_pk₂,₂        0.091537          0.070162          [  4.0211e-9 ;   0.22477   ]
Ω_pk₃,₃        0.055024          0.033284          [  5.8373e-9 ;   0.10965   ]
Ω_pk₄,₄        2.9089e-74        3.9371e-90        [  2.9089e-74;   2.9089e-74]
σ_prop_pk      0.00084244        4.2317e-7         [  0.00084171;   0.00084318]
σ_add_pk       0.53685           0.025487          [  0.48387   ;   0.58449   ]
tvturn         9.8483            0.51322           [  8.4322    ;  10.511     ]
tvebase       11.016             0.5216            [ 10.117     ;  12.141     ]
tvec50         0.28956           0.030112          [  0.24576   ;   0.3583    ]
Ω_pd₁,₁        0.025593          0.0080927         [  0.0067727 ;   0.039601  ]
σ_add_pd       0.21128           0.015438          [  0.17598   ;   0.23344   ]
--------------------------------------------------------------------------------
Successful fits: 200 out of 200
Unique resampled populations: 200
No stratification.

You can also convert the Bootstrap inference results to a DataFrame with coeftable:

coeftable(infer_boot_2cmt_lin_turnover)

Conclusion

This tutorial covered the basic workflow of constructing a model, simulating observations from it, and conducting parameter estimation. You can also see subsequent tutorials that discuss the components in more detail, such as:

1. More detailed treatment of specifying populations, dosage regimens, and covariates.
2. Reading in dosage regimens and observations from standard input data.
3. Fitting models with different estimation methods.